Equilibria
Factors affecting chemical equilibria
In chemistry, equilibrium refers to chemical reactions that are in balance. The  sign is used to represent a reaction in equilibrium. You need to know the following.
sign is used to represent a reaction in equilibrium. You need to know the following.
• All chemical reactions are reversible, given enough energy.
• In a reversible reaction at equilibrium, the rates of the forward and backward reactions are the same. In other words, the amount of reactants forming products in a given time is the same as the amount of products breaking down to give reactants in the same time. These are generally called dynamic equilibria.
An example of a dynamic equilibrium established in the gas phase is the reaction of nitrogen and hydrogen to form ammonia in the Haber process:

Dynamic equilibria can also happen in the liquid phase:

In a dynamic equilibrium:
- There is no net change in the concentration of each substance.
- The equilibrium compositions of the substances can be approached from either reactants or products.
Le Chatelier’s principle
The French chemist Henri le Chatelier studied many dynamic equilibria and suggested a general rule, Le Chatelier’s principle, to help predict the changes in the position of equilibrium as different factors are changed.
Le Chatelier’s principle states that if a closed system at equilibrium is subject to a change, then the system will adjust in such a way so as to minimise the effect of the change.
The factors that can be changed easily are concentration, temperature and pressure. You might also have suggested using a catalyst – this possibility is looked at later.
Consider a general reaction:

If you increase the concentration of either of the reactants A or B, more of the products C and D will be made.
The general reaction shown above is an exothermic reaction. If you increase the temperature, there will be less of the products made. The reverse would be true for an endothermic reaction.
The influence of pressure is relevant only for gas phase reactions. Think about the Haber process for making ammonia

There are fewer molecules on the right-hand side of the equation. This means that if you increase the pressure, the equilibrium will shift to produce more ammonia, reducing the total number of molecules in the system and therefore reducing the pressure.
In order to see what effect adding a catalyst might have, you have to think about the processes taking place. Graph which shows the energy profile of an equilibrium reaction with and without a catalyst present.

Reaction profile with and without a catalyst shows that the catalyst has lowered the activation energy for the forward reaction. Consider the reverse reaction – the activation energy for this has also been lowered by the same amount. In other words, the presence of a catalyst does not change the position of equilibrium; it enables equilibrium to be established more quickly.
Equilibrium constants and calculations
Using Kc
For any equilibrium in the liquid state an equilibrium constant, Kc, can be defined in terms of concentration. For our general equation:

For equilibria involving liquids use Kc for the equilibrium constant, but for gas phase reactions use Kp.
The quantities in square brackets represent the concentrations of the different species at equilibrium. It is also important to remember that equilibrium constants depend on temperature.
For gas phase reactions, partial pressures (in atmospheres) of the species involved in the equilibrium are used. To distinguish this from reactions in solution, the symbol Kp is used for the equilibrium constant. So, for the reaction between hydrogen and iodine to form hydrogen iodide:

where p represents the partial pressure of each of the species.
Look at how these two constants are calculated.
Using Kp
You can use a similar process to calculate Kp for reactions taking place in the gas phase. To do this you need to understand what is meant by partial pressure.
The partial pressure of a gas is its mole fraction multiplied by the total pressure.
Suppose we think of air as consisting of one-fifth oxygen and four-fifths nitrogen at a total pressure of 100 kPa:


Together this gives the total pressure of 100 kPa.
The Haber process
In the Haber (or Haber–Bosch) process, ammonia is produced on a massive scale using nitrogen from the air and hydrogen from the reaction of methane, CH4, with steam:

To make the process as economic as possible, the conditions needed are:
• a high equilibrium concentration of ammonia
• equilibrium to be reached in a short period of time
To understand the conditions chosen you need to know more about the reaction:
• At 298 K the equilibrium constant is very large, but only a tiny amount of ammonia is produced at this temperature because the rates of the forward and backward reactions are so low that equilibrium is never reached.
• Increasing the temperature increases the rates of both reactions but drastically reduces the equilibrium constant because the reaction is exothermic.
• Increasing the partial pressures of the reactants increases the equilibrium concentration of ammonia – for example, using 7500 kPa of hydrogen and 2500 kPa of nitrogen at 798 K gives a conversion with about 10% of ammonia at equilibrium.
The solution is to use an iron catalyst to increase the rate of attaining equilibrium, and then to use a compromise set of conditions – a relatively low temperature (around 750 K) and a moderately high pressure (20 000 kPa). The equilibrium mixture is then passed through a heat exchanger to cool and liquefy the ammonia, which is removed – the unreacted nitrogen and hydrogen are recycled.
The Contact process
The key stage in the production of sulfuric acid relies on an equilibrium reaction. In this process, sulfur dioxide is reacted with oxygen to form sulfur trioxide:

The forward reaction is exothermic. Therefore, Le Chatelier’s principle predicts that cooling the reaction mixture would give an increased yield. However, as you saw in the Haber process, this reduces the rate of attaining equilibrium.
Because there is an overall reduction in the number of molecules moving from left to right, Le Chatelier’s principle also predicts that increasing the pressure will drive the equilibrium to the right, increasing the yield of sulfur trioxide.
The conditions used mirror these principles. The gas mixture is passed over three catalyst beds and is cooled after each pass to try to force the equilibrium to the right. Although a higher pressure is predicted to push the equilibrium to the right, most chemical plants producing sulfuric acid operate at just above atmospheric pressure to reduce costs.
Ionic equilibria
Brønsted–Lowry acids and bases
The Brønsted–Lowry theory is the most commonly used description of acidity. It describes an acid as a substance capable of donating protons (H+) and a base as a substance capable of accepting them:
HCl + NH3 → Cl− + NH4+
• In this reaction hydrogen chloride is acting as an acid by donating a proton to ammonia, which is acting as a base.
• In the reverse of this reaction, the chloride ion accepts a proton from the ammonium ion. This means that the ammonium ion would be acting as an acid in donating the proton to the chloride ion, which would be acting as a base.
• In this reaction, the chloride ion is known as the conjugate base of hydrogen chloride and the ammonium ion as the conjugate acid of ammonia.
Conjugate acid–base pairs In the Bronsted-Lowry theory an acid produces a conjugate base. For example, HCl forms a proton, H+, and a chloride ion, Cl−. The chloride ion is the conjugate base of HCl. In a similar way, bases form conjugate acids, e.g. NH3 + H2O → NH4+ + OH−
Here, NH4+ is the conjugate acid of NH3.
It is also important to know how substances behave with water, the common solvent. Hydrogen chloride reacts with water:
HCl + H2O → Cl− + H3O+
Here water is acting as a base, accepting a proton from hydrogen chloride; the H3O+ ion is its conjugate acid.
Water also reacts with ammonia:
H2O + NH3 → OH− + NH4+
Water is acting as an acid, donating a proton to ammonia; the OH− ion is its conjugate base.
Strong and weak acids and bases
It is important to understand the difference between dilute and weak, and concentrated and strong when you are writing about acids and bases:
- A strong acid or strong base is completely ionised in solution. We often refer to the compound as being completely dissociated.
- A weak acid or weak base is only partially ionised in solution. We often refer to the compound as being partly dissociated.
- A concentrated acid or concentrated base has a large number of moles per unit volume of the acid or base.
- A dilute solution has a small number of moles relative to the solvent.
Examples of strong and weak acids and bases are shown below
| Acids | Bases | ||||||
| Strong | pH | Weak | pH | Strong | pH | Weak | pH |
| HCl | 1 | CH3CO2H | 3 | NaOH | 14 | NH3 | 11 |
| HNO3 | 1 | H2CO3 | 4 | KOH | 14 | CH3NH2 | 12 |
| H2SO4 | 1 | H2O | 7 | Ca(OH)2 | 12 | H2O | 7 |
The pH values are given to the nearest whole number for 0.1 mol dm−3 solutions.
The categories ‘strong’ and ‘weak’ are qualitative. To be accurate you need to be able to make quantitative comparisons using dissociation constants or the pH values of solutions of the compounds.
When an acid, HA, dissolves in water, the equilibrium established is:

The position of the equilibrium depends the strength of the acid. For a strong acid, the equilibrium favours the products, and the reaction goes almost to completion. For a weak acid, the equilibrium favours the reactants, with relatively few H+(aq) ions being produced.
A more precise indication of the position of equilibrium can be obtained by working out an equilibrium constant:

[H2O(l)] is in excess and is almost constant, so you use a new equilibrium constant called the acid dissociation constant, Ka, which includes this and has units mol dm−3.
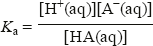
Values of Ka are small (especially for weak acids and bases) and it is usual to convert them to a logarithm (to base 10) of their value (pKa), as with [H+(aq)] and pH.
Consider water at 298 K. The concentration of H+(aq) ions is 10−7 mol dm−3:
pH = −log[H+(aq)]
pH = −log(10−7) = 7
The numbers are not always this simple. Suppose that in a given solution [H+(aq)] = 8.6 × 10−9 mol dm–3.
To calculate the pH of this solution you need to understand how to work out the logarithm of this sort of number:

You can also calculate [H+(aq)] given the pH of a solution. A solution with a pH of 2.73 has its hydrogen ion concentration worked out like this:

Another piece of information that is useful is the ionic product of water, Kw. This is the product of [H+(aq)] and [OH–(aq)] and at 298 K is equal to 10−14 mol2 dm–6. This enables us to calculate [OH–(aq)] as well as [H+(aq)] in any aqueous solution.
Choosing indicators for titrations
When carrying out a titration, it is the pH of the solution at the end point that is critical when choosing a suitable indicator. Two main factors need to be considered:
- The colour change should be sharp – no more than one drop of acid or alkali should give a distinct colour change.
- The end point should occur when the solution contains the same number of hydrogen ions as hydroxide ions.
Plotting graphs of the change in pH with the addition of the titrating solution produces different curves for combinations of weak and strong acids with weak and strong bases, as Figure 7.2 shows.

Figure 7.2 Titration curves for (a) a strong acid with a strong base, (b) a weak acid with a strong base, (c) a strong acid with a weak base, (d) a weak acid with a weak base
- Figure 7.2(a) shows the change in pH during the titration of a 25 cm3 sample of 0.1 mol dm−3 strong acid when adding strong base. Notice that there is a long vertical portion at 25 cm3 showing a large change in pH.
- 6 What is the pH of:
- a a solution containing 10−5 mol dm−3 H+(aq)
- b a solution containing 10−3.5 mol dm−3 H+(aq)
- c a solution containing 10−5.5 mol dm−3 OH−(aq)?
Choosing indicators for titrations
When carrying out a titration, it is the pH of the solution at the end point that is critical when choosing a suitable indicator. Two main factors need to be considered:
- The colour change should be sharp – no more than one drop of acid or alkali should give a distinct colour change.
- The end point should occur when the solution contains the same number of hydrogen ions as hydroxide ions.
Plotting graphs of the change in pH with the addition of the titrating solution produces different curves for combinations of weak and strong acids with weak and strong bases, as Figure 7.2 shows.

Figure 7.2 Titration curves for (a) a strong acid with a strong base, (b) a weak acid with a strong base, (c) a strong acid with a weak base, (d) a weak acid with a weak base
- Figure 7.2(a) shows the change in pH during the titration of a 25 cm3 sample of 0.1 mol dm−3 strong acid when adding strong base. Notice that there is a long vertical portion at 25 cm3 showing a large change in pH.
- Figure 7.2(b) shows the change in pH during the titration of a 25 cm3 sample of 0.1 mol dm−3 weak acid when adding strong base. Notice that, although the vertical portion occurs at 25 cm3, it is shorter and it starts at a higher pH than in (a).
- Figure 7.2(c) shows the change in pH during the titration of a 25 cm3 sample of 0.1 mol dm−3 strong acid when adding weak base. Notice that, although the vertical portion occurs at 25 cm3, it is shorter and it starts at a lower pH than (a).
- Figure 7.2(d) shows the change in pH during the titration of a 25 cm3 sample of 0.1 mol dm−3 weak acid when adding weak base. Notice that now the vertical portion has practically disappeared, but it is closer to pH 7.
The vertical portion of the pH versus volume graph has to be in the pH range of the indicator to give a colour change.The diagrams also show the effective ranges of two common indicators – phenolphthalein and methyl orange. Table below shows the choice of indicator for the four titrations shown in Figure 7.2. Study the diagrams and try to decide on the reasons for the choices.
|
Acid/base combination |
Indicator used |
|
Strong acid/strong base |
Either would do |
|
Weak acid/strong base |
Phenolphthalein |
|
Strong acid/weak base |
Methyl orange |
|
Weak acid/weak base |
Neither is suitable; a different method is needed |
Buffer solutions
Buffer solutions are able to resist a change in acidity or alkalinity, maintaining an almost constant pH, when a small amount of either substance is added. An important example of such a system occurs in blood, the pH of which is kept close to 7.4 by the presence of hydrogencarbonate ions, HCO3−.
A buffer solution is a solution that can resist changes in acidity or alkalinity.
Buffers rely on the dissociation of weak acids. Consider the weak acid HA:
HA(aq) ⇌ H+(aq) + A−(aq)
Because it is a weak acid, [H+(aq)] is about equal to [A−(aq)] and is very small. If a small amount of an alkali is added, the OH− ions react with the H+ ions, removing them from the solution as water molecules and this disturbs the equilibrium.
By Le Chatelier’s principle, more HA will dissociate to restore the equilibrium, maintaining the pH. On the other hand, if some acid is added, the H+ ions will react with the A− ions, forming more HA. However [A−(aq)] is very low and it would soon be used up.
This problem is solved by adding more A− ions in the form of a salt of the acid HA, such as Na+A−. Now there are more A− ions to ‘mop up’ any added H+ ions. So a buffer solution consists of a weak acid and a salt of that weak acid.
In the case of the buffer system in blood, the equilibrium is:
H+(aq) + HCO3−(aq) ⇌ CO2(aq) + H2O(l)
Addition of H+ ions moves the equilibrium to the right, forming more carbon dioxide and water, while the addition of OH− ions removes H+ ions causing the equilibrium to move to the left, releasing more H+ ions.
To calculate the pH of a buffer you can use the expression:

In other words, you need to know the pKa of the acid, together with the concentrations of the acid and its salt in the solution.
WORKED EXAMPLE
Calculate the pH of an ethanoate–ethanoic acid buffer made by mixing 25 cm3 of 0.100 mol dm−3 sodium ethanoate solution with 25 cm3 of 0.100 mol dm−3 ethanoic acid solution. Ka for ethanoic acid is 1.8 × 10−5 mol dm−3.
Answer
Mixing the two solutions means that the total volume is 50 cm3, so the concentration of each is halved. Substituting these values in the equation gives:
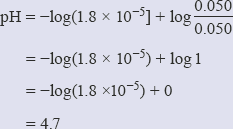
Solubility product
Another application of equilibrium involves the solubility of sparingly soluble salts. All the applications looked at so far have involved homogeneous equilibria (all the substances in the same phase). With sparingly soluble substances there are heterogeneous equilibria to consider, with one component in the solid phase and the remainder in the aqueous phase.
For example, in a saturated solution of silver chloride this equilibrium exists:
AgCl(s) ⇌ Ag+(aq) + Cl−(aq)
The equilibrium constant for this system can be written as

However, it is not possible to change the concentration of a solid, so a new equilibrium constant is defined that allows for this. This is called the solubility product, Ksp, and is the product of the concentrations of the ions present in solution:
Ksp = [Ag+(aq)][Cl−(aq)]
In this case, the units of Ksp are mol2 dm−6.
WORKED EXAMPLE
Suppose you want to know if a precipitate will form when you mix equal quantities of solutions of silver nitrate and potassium chloride. Let us assume that the concentration of potassium chloride is 1.0 × 10−3 mol dm−3 and that of silver nitrate is 1.0 × 10−5 mol dm−3. Ksp for silver chloride at 298 K is 1.8 × 10–10 mol2 dm−6.
Answer
On mixing equal quantities of the two solutions, each concentration is halved. Substituting the numbers into the expression for Ksp gives:
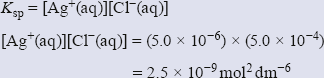
This is higher than 1.8 × 10−10 mol2 dm−6 so a precipitate will form.
This same method can be used to calculate the concentration of one ion if you know that of the other ion along with the relevant Ksp. It is also important to remember to write out the equilibrium equation and expression because not all salts have a 1 : 1 ratio of ions.
If a substance is added that has an ion in common with the sparingly soluble salt, the concentration of that ion affects the equilibrium. This is known as the common ion effect.
So, if sodium chloride solution is added to a saturated solution of silver chloride:
AgCl(s) ⇌ Ag+(aq) + Cl−(aq)
more solid is precipitated. This is because the added chloride ions push the equilibrium backwards, according to Le Chatelier’s principle.
Partition coefficients
You are familiar with water as a solvent, but many other liquids also act as solvents:
• In general, substances dissolve when the energy of the solute–solvent system is lower when the solute is dissolved than when the solute is not dissolved.
• This is usually the case if the interactions between the solute particles and the solvent molecules are similar to those between the solvent molecules themselves.
Molecules can attract each other in a variety of ways:
• ionic attractions
• ion–dipole attractions
• hydrogen bonding
• van der Waals’ forces
As a general rule:
• Polar solvents are more likely to dissolve ionic compounds, substances that form hydrogen bonds and/or molecules with dipoles.
• Non-polar solvents dissolve solutes that have molecules attracted to each other by only van der Waals’ forces.
Partition for a non-polar solvent
Iodine is a molecular solid and is unlikely to be as soluble in water (polar solvent) as it is in hexane (non-polar solvent). If some iodine crystals are shaken with a mixture of water and hexane until no further change occurs, the iodine distributes itself between the two solvents according to its solubility in each.
On measuring the amount of iodine dissolved in each solvent, you find that the ratio of the concentrations is constant, no matter how much iodine is used. This constant is known as the partition coefficient, Kpc:

Here, Kpc is an equilibrium constant for the dissolving of iodine in the two solvents. Partition coefficients have no units.
WORKED EXAMPLE
0.95 g of iodine (Mr = 254) was shaken with a mixture of 50 cm3 of water and 50 cm3 of tetrachloromethane. The organic layer was run off, and the aqueous layer titrated with standard 0.01 mol dm−3 sodium thiosulfate solution. 25.0 cm3 of the aqueous layer required 4.30 cm3 of thiosulfate for complete reaction. Calculate the partition coefficient of iodine between water and tetrachloromethane.
2S2O32−(aq) + I2(aq) ⇌ S4O62−(aq) + 2I−(aq)
Answer
