Reaction kinetics
Simple rate equations
The rates of chemical reactions are affected by three main conditions:
• temperature
• concentration
• presence of a catalyst
A reaction cannot take place unless the reacting particles collide with sufficient energy.
• Not all collisions result in changes and the minimum energy required is called the activation energy, Ea.
• Increasing the temperature increases the proportion of successful collisions.
• Increasing the concentration increases the chance of collisions taking place.
• In the presence of a catalyst, a reaction has a different mechanism – one of lower activation energy, giving more successful collisions.
Boltzmann distribution of energies
The energy of molecules is directly proportional to their absolute temperature. The graph below shows a typical distribution of energies at constant temperature. This is known as the Boltzmann distribution.

Boltzmann distribution
There are a number of points to remember about this graph:
• The distribution always goes through the origin.
• The curve approaches the x-axis but does not touch it.
• The peak represents the most probable energy.
• The area under the curve represents the total number of particles.
• Ea represents the activation energy (the minimum energy needed for reaction). The shaded portion represents the number of particles with energy higher than or equal to the activation energy (E ≥ Ea).
The effect of temperature
An increase in temperature changes the shape of the Boltzmann distribution curve as shown in
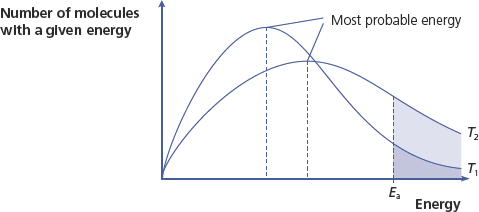
Boltzmann distribution at different temperatures
Notice that only the temperature has changed, so the areas under the two curves are the same. The graph shows that at a higher temperature, T2:
• There are fewer particles with lower energy (the curve is flatter).
• The most probable energy is higher.
• More particles have E ≥ Ea.
At higher temperature, a greater proportion of particles have sufficient energy to react, and hence the rate of reaction increases. The reverse is true at lower temperatures.
The effect of concentration
The Boltzmann distribution is not relevant here. The explanation given at the beginning of the chapter in terms of increasing the chance of collisions is adequate. It is worth remembering that increasing the pressure of a gas phase reaction has the same effect as increasing concentration in the liquid phase.
The effect of a catalyst
Remember that catalysts speed up chemical reactions without being permanently changed themselves. In the presence of a catalyst, a reaction has a different mechanism with a different activation energy, Ecat.
Practice questions

Activation energy in the presence and absence of a catalyst
Catalysis is the process whereby the activation energy of a reaction is lowered by the presence of another element or compound.
It is important to remember that catalysts do not change the Boltzmann distribution for the temperature concerned. In a reaction that is speeded up, the position of Ea simply moves to the left, increasing the proportion of particles with E ≥ Ea, as shown below

Practice Questions
- explain the terms rate of reaction, frequency of collisions and effective collisions
- define activation energy, Ea, and sketch and use the Boltzmann distribution to explain its significance and the effect of temperature on reaction rates
- construct and interpret a reaction pathway diagram showing the effect of the presence of a catalyst
Order of reaction
To describe rate relationships in a reaction mathematically, a rate equation is used. These have the form:
rate = k[A]m[B]n
• Here, k is the rate constant for the reaction between substances A and B, and m and n are the powers to which the concentrations of these substances are raised in the experimentally determined rate equation.
• Each is called the order with respect to each substance. For the reactions in A Level work, m and n can be 0, 1 or 2.
• It is important to remember that not all reactions take place in a single step.
• For multi-step reactions, one step will always be slower than all the others. This is called the rate-determining step, because it is on this that the overall reaction rate depends.
The rate-determining step is the slowest step in a multi-step reaction and the overall reaction rate depends on this.
It is easier to understand what this means by looking at some examples. Consider the reaction:
A + B → products
If you measure the way in which the rate of this reaction changes depending on the concentrations of A and B, you might find that doubling the concentration of A doubles the rate. You might also find that doubling the concentration of B doubles the rate.
This tells us that the order with respect to A is 1, and that the order with respect to B is also 1 – so the overall order of the reaction is 2. The rate equation could be written:
rate = k[A]1[B]1
However, you do not need to show m and n when they are 1:
rate =k[A][B]
In another reaction:
X + Y → products
the rate might not depend on Y reacting with X, but on X breaking down and then Y reacting with those products. When this is the case, the rate equation has the form:
rate = k[X]1[Y]0
Remembering that anything to the power 0 equals 1, this rate equation can be written:
rate = k[X]
Deducing order by the initial rates method
Most reaction kinetic studies are based on experimental work. Consider a reaction for which the rate can be measured at the start. Data from such an experiment are given in table
| Run | Initial [A]/mol dm−3 | Initial [B]/mol dm−3 | Initial rate/mol dm−3 s−1 |
| 1 | 1.00 | 1.00 | 1.25 × 10−2 |
| 2 | 1.00 | 2.00 | 2.5 × 10−2 |
| 3 | 2.00 | 2.00 | 2.5 × 10−2 |
Look at runs 1 and 2 – if you double the concentration of B and keep the concentration of A constant, then the rate doubles. Look at runs 2 and 3 – doubling the concentration of A and keeping the concentration of B constant has no effect on the rate. This tells us that the reaction is first order with respect to B and zero order with respect to A. In other words, A does not feature in the rate equation. You can now calculate the rate constant:
rate = k[B]
2.5 × 10−2 mol dm−3 s–1 = k × 2.0 mol dm−3
k = 1.25 × 10−2 s−1
Deducing order from graphs
Another way of deducing the order of a reaction with respect to a given reagent is to look at a graph of concentration against time. Zero-order and first-order reactions have characteristic shapes.

Concentration–time graphs for (a) a zero-order reaction and (b) a first-order reaction
It is also possible to compare graphs of rate against concentration.

Rate–concentration graphs of (a) a zero-order reaction and (b) a first-order reaction
These graphs show that in a zero-order reaction, the rate is independent of concentration and gives a horizontal line. For a first-order reaction, the reaction shows a constant time for the concentration of a reactant to halve. This is known as the half-life of the reaction and is similar to the half-life concept in radioactive decay.
A half-life can be used to calculate the rate constant of a reaction. Look at this reaction:
CH3N2CH3(g) → C2H6(g) + N2(g)
When the compound is heated it decomposes into the two gases shown. No other reactants are needed so:
rate = k[CH3N2CH3(g)]
The half-life of this reaction at 500 K is about 1750 s. This means that if the starting concentration is 0.10 mol dm–3, after 1750 s the concentration will have halved to 0.05 mol dm−3. After another 1750 s, the concentration will have halved to 0.025 mol dm−3, and so on.
A half-life can be used to calculate the rate constant, k. For a first-order reaction:

Multi-step reactions and predicting order
Reactions can happen in a single step or more than one step (multi-steps). For the examination, you need to be able to predict the order of a reaction from a given mechanism (and vice versa).
Consider this reaction of a primary halogenoalkane:
C4H9Br + OH− → C4H9OH + Br−
This could occur in one step as shown above or in two steps:
slow step: C4H9Br → C4H9+ + Br−
fast step: C4H9+ + OH– → C4H9OH
• If the first mechanism is correct, you would predict that the reaction is first order with respect to both C4H9Br and OH−.
• If the second mechanism is correct you would predict that the reaction is first order with respect to only C4H9Br, because this is the rate-determining step.
• The slowest step is always the one (bottleneck) that determines the rate (the rate-determining step).
• In this example, practical evidence suggests that the first mechanism is correct.
Experimental techniques for studying rates
It is important to consider the methods that are available to follow the progress of a reaction and to determine the rate.
Sampling followed by titration
Small amounts of the reaction mixture are withdrawn by pipette at regular intervals. Further reaction in this sample is prevented, often by adding a large volume of a common inert solvent. The concentration of one of the reactants or products is then determined by titration of the samples. Common examples are the formation of an acid and an iodination reaction
Using a colorimeter
This method only works if one of the reactants or products is coloured. It has advantages over titration in that no sampling is needed and it gives an almost instantaneous result. An example is the formation of a transition metal complex.
Measurement of gas evolved
One of the products has to be a gas for this method to work. The volume of the gas is measured in a syringe or by the displacement of water from an upturned burette. An example is the reaction between an acid and a carbonate.
Catalysis
You will already have come across the use of catalysts in your GCSE work. You need to know how catalysts are able to speed up reactions. Catalysts can be:
• homogeneous (in the same physical state as the reactants)
• heterogeneous (in a different physical state from the reactants)
The Haber process
The catalyst is heterogeneous – in a different phase from the gases. Transition metals are particularly good at acting as catalysts because their atoms have unfilled d-orbitals. The gases are adsorbed onto the surface of the metal, forming weak bonds. This can have one of two consequences:
- • The formation of bonds with the metal surface may weaken the bonds within the gas molecules.
- • The orientation of the adsorbed molecules may be favourable for the reaction.
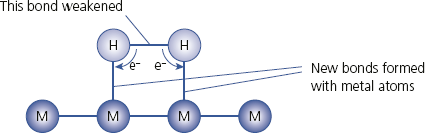
Adsorption of a gas onto the surface of a metal catalyst
Catalytic converters in vehicle exhausts
• Catalytic converters have become important in recent years – they are designed to remove pollutant gases from vehicle exhausts.
• The problem is complex because some pollutants, such as carbon monoxide, have to be oxidised while others, such as nitrogen oxides, have to be reduced.
• The converter consists of a ceramic honeycomb with a very thin coat of platinum, rhodium and palladium (all expensive metals). The platinum and rhodium help to reduce the NOx to nitrogen, while platinum and palladium help to oxidise the CO and unburnt hydrocarbons to carbon dioxide and water.
• The car has to run on unleaded petrol because lead would ‘poison’ the catalyst, making it ineffective.
• This is a heterogeneous system.
Nitrogen oxides in the atmosphere
• Nitrogen(IV) oxide is unchanged by the reaction and is thought to form a weak intermediate with sulfur dioxide.
• This is an example of homogeneous catalysis – the reactants and the catalyst are in the same phase, in this case gases.
• Studies on acid rain have shown that in the atmosphere the presence of oxides of nitrogen, particularly nitrogen(IV) oxide (NO2), increases the rate of oxidation of sulfur dioxide to sulfur trioxide.
The role of Fe2+ in the I−/S2O82− reaction
The oxidation of iodide ions by peroxodisulfate ions is another example of homogeneous catalysis. In this case, all the species are in the aqueous phase. It is believed that this oxidation occurs in two steps in the presence of Fe3+ ions:
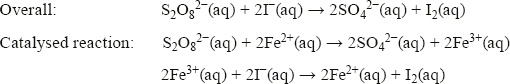
Although there are two steps in the reaction, the overall activation energy is lower than in the single-step reaction, as can be seen in

The effect of a catalyst on a reaction profile.
Practice questions
- explain and use the terms rate equation, order of reaction, overall order of reaction, rate constant, half-life, rate-determining step and intermediate
- understand and use rate equations of the form rate = k[A]m[B]n for which m and n are 0, 1 or 2; deduce the order of a reaction from concentration–time graphs or from experimental data from an initial rates or half-life method; calculate an initial rate from concentration data; construct a rate equation
- show understanding that the half-life of a first-order reaction is independent of concentration and use the half-life of a first-order reaction in calculations
-
calculate the numerical value of a rate constant using the initial rates and the rate equation; using half-life and the equation

- for a multi-step reaction suggest a reaction mechanism consistent with the rate equation; predict the order that would result from a given mechanism and rate-determining step; deduce a rate equation using a given mechanism and rate-determining step; identify an intermediate or catalyst and the rate-determining step from a given mechanism
- describe qualitatively the effect of temperature change on the rate constant and hence the rate of reaction
- explain that catalysts can be homogeneous or heterogeneous
- describe the mode of action of a heterogeneous catalyst, e.g. iron in the Haber process; palladium, platinum and rhodium in catalytic converters in exhaust systems
- describe the mode of action of a homogeneous catalyst, e.g. atmospheric oxides of nitrogen in oxidising atmospheric sulfur dioxide; Fe2+ and Fe3+ in the I−/S2O82− reaction
6 Comments
Vind hier de meest betaalbare opties bij een online internetapotheek
April 1, 2024provera online kopen in Breda
aankoop van medroxyprogesterone in Martinique
koop provera in Antwerpen
medroxyprogesterone bestellen zonder voorschrift: legaal en veilig medroxyprogesterone
verkrijgbaar in Haarlem – bestel nu en ontvang snel.
provera online bestellen: Snelle levering gegarandeerd provera
online bestellen: de slimme keuze voor moderne consumenten
medroxyprogesterone kopen zonder recept: snel en gemakkelijk medroxyprogesterone kopen zonder voorschrift in Nederland.
prijs van medroxyprogesterone in de apotheek medroxyprogesterone kopen:
geen gedoe, gewoon bestellen en thuis laten bezorgen.
medroxyprogesterone bestellen met gratis verzending
medroxyprogesterone discreet verzonden
provera kopen tegen de beste prijs medroxyprogesterone te koop in Nederland zonder
recept
prijs van provera in een apotheek in Nederland
Veilige online aankoop van medroxyprogesterone in Nederland Beste prijzen voor medroxyprogesterone zonder voorschrift online
Koop provera zonder voorschrift in Maastricht – veilig en discreet.
provera online te bestellen
beschikbaarheid van medroxyprogesterone in Rotterdam medroxyprogesterone bestellen zonder voorschrift: betrouwbaar en discreet
provera online korting in Nederland
medroxyprogesterone online verkrijgbaar in heel Nederland
Gemakkelijk provera bestellen in Almere – geen gedoe meer
met apotheken.
medroxyprogesterone online aankoop in Delft medroxyprogesterone bestellen zonder recept online
Ontvang medroxyprogesterone snel en eenvoudig bij u
thuis in Nederland medroxyprogesterone beschikbaar in verschillende
formaten
medroxyprogesterone vrij verkrijgbaar in Spanje
provera online aanschaffen voor een scherpe prijs medroxyprogesterone verzending en bezorgopties
in Nederland
waar provera zonder recept kopen medroxyprogesterone verkrijgbaar in Leeuwarden – bestel vandaag nog!
Wo kann ich cefadroxil in den Niederlanden finden
April 3, 2024I have read so many articles regarding the blogger lovers except this piece
of writing is in fact a pleasant article, keep it up.
online verkoop van alli in Frankrijk
April 5, 2024Good post. I learn something totally new and challenging on websites I stumbleupon every day.
It will always be useful to read content from other writers and practice a little something from their websites.
comprar benadryl en Europa
April 11, 2024There’s certainly a great deal to find out about this subject.
I really like all the points you’ve made.
waar allopurinol kopen
April 12, 2024My family all the time say that I am killing my time here at net, except I
know I am getting knowledge everyday by reading such fastidious articles.
Obie Tremblay
June 19, 2024미 소비자심 메이저사이트 리 부진에 시장에선 연 2회 금리인하 기대감이 유지됐다